Seminal blog post of Yarin Gal from Cambridge machine learning group What my deep model doesn't know... motivated me to learn how Dropout can be used to describe the uncertainty in my deep learning model.
This blog post is dedicated to learn how to use Dropout to measure the uncertainty using Keras framework.
import matplotlib.pyplot as plt
import tensorflow as tf
from keras.backend.tensorflow_backend import set_session
import keras
import sys, time, os, warnings
import numpy as np
import pandas as pd
from collections import Counter
warnings.filterwarnings("ignore")
print("python {}".format(sys.version))
print("keras version {}".format(keras.__version__)); del keras
print("tensorflow version {}".format(tf.__version__))
config = tf.ConfigProto()
config.gpu_options.per_process_gpu_memory_fraction = 0.5
config.gpu_options.visible_device_list = "4"
set_session(tf.Session(config=config))
Review Dropout¶
First, I will review how Keras defines the dropout by creating very simple NN architecture with dropout. Then, I will make sure that the output of hand-made NN agrees to the output of Keras's NN with dropout.
For simplicity, I create two-layer feed-forward NN with dropout by hand (i.e., 1 hidden layer and 1 output layer.). The input and output dimentions are only 1 and the NN contains only one hidden layer with two hidden units. This model only contains 7 parameters (See below). The hidden layer is followed by the dropout with dropout rate 0.7.
Dropout in Keras¶
Dropout in Keras with tensorflow backend is defined here and it essentially calls for tf.nn.dropout. The documentation of tf.nn.dropout says:
Computes dropout. With probability keep_prob, outputs the input element scaled up by 1 / keep_prob, otherwise outputs 0. The scaling is so that the expected sum is unchanged. By default, each element is kept or dropped independently.
Therefore, you can think of the dropout as the scaled random vector from Bernoulli distribution with dropout rate as the success probability. The random vector is scaled by 1/(1 - dropout rate). The length of the random vector is the same as the number of hidden units on the hidden layer prior to the dropout layer. If the number of hidden units is 2 in the prior layer, then the random vector of the dropout is defined as: $$ \boldsymbol{I}=[I_1,I_2]\\ I_k \overset{i.i.d.}{\sim} \textrm{Ber}(p_{\textrm{dropout}})\\ k = 1,2 $$ where $*$ is an element wise multiplication.
The 2 layer NN definition¶
Formally I can define my simple NN with dropout in two line as: $$ \boldsymbol{h}_1 = \textrm{relu}( x \boldsymbol{W}_1 + \boldsymbol{b}_1)\\ y = (\boldsymbol{h}_1 * \boldsymbol{I})\boldsymbol{W}_2 + \boldsymbol{b}_2 $$ where:
- Input: 1x1 matrix: $x \in R^{1x1}$
- output: 1x1 matrix: $y \in R^{1x1}$
- Parameters: $ \boldsymbol{W}_1 \in R^{1 x 2}, \boldsymbol{b}_1 \in R^{1 x 2} \\ \boldsymbol{W}_2 \in R^{2 x 1}, \boldsymbol{b}_1 \in R^{1 x 1} $
Notice that bias does not get dropped out.
Assign values to parameters¶
We will provide values to the weights and biases as follows:
import numpy as np
w1, b1 = np.array([3,7]).reshape(1,2), np.array([5,1]).reshape(2)
w2, b2 = np.array([-10,10]).reshape(2,1), np.array([11]).reshape(1)
print("w1={},\nb1={},\nw2={},\nb2={}".format(w1,b1,w2,b2))
weights = ((w1,b1), (w2,b2))
Define the 2 layer NN with dropout in python.
def relu(x):
x[ x < 0 ] = 0
return(x)
def NN2layer_dropout(x,weights,p_dropout=0.1):
## rate: float between 0 and 1. Fraction of the input units to drop.
(w1,b1), (w2,b2) = weights
## dropout
keep_prob = 1 - p_dropout
Nh1 = w2.shape[0]
Ikeep = np.random.binomial(1,keep_prob,size=Nh1)
I = np.zeros((1,Nh1))
I[:,Ikeep==1] = 1/keep_prob
## 2-layer NN with Dropout
h1 = relu(np.dot(x,w1) + b1)
y = np.dot(h1*I,w2) + b2
return(y[0,0])
Define 1-d input.¶
Here I only consider a single sample. x is defined as:
x = np.array([2]).reshape(1,1)
Using the defined NN, I will predict the y value corresponding to this x using dropout. AS we define the dropout rate to be 0.7, I expect there are four possible predicted value for this x with the distribution as:
| $\boldsymbol{I}$ | probability | $y$ value |
|---|---|---|
| [0, 0] | 0.3 x 0.3=0.09 | 144 |
| [1, 0] | 0.7 x 0.3=0.21 | -355 |
| [0, 1] | 0.3 x 0.7=0.21 | 511 |
| [1, 1] | 0.7 x 0.7=0.49 | 11 |
The script below generate predicted value of y 1,000 times, and plot its histogram. The distribution of predicted y more or less agree to the table above.
from collections import Counter, OrderedDict
def plot_histogram(ys, ax, title=""):
counter = Counter(ys)
counter = OrderedDict(sorted(counter.items()))
probs = np.array(counter.values())*100.0/np.sum(counter.values())
keys = np.array(counter.keys())
print(title)
for k,p in zip(keys,probs):
print("{:8.2f}: {:5.2f}%".format(k,p))
n, bins, rect = ax.hist(ys)
ax.set_title(title)
ax.grid(True)
Nsim = 1000
p_dropout = 0.7
ys_handmade = []
for _ in range(Nsim):
ys_handmade.append(NN2layer_dropout(x,weights,p_dropout))
fig = plt.figure(figsize=(6,2))
ax = fig.add_subplot(1,1,1)
plot_histogram(ys_handmade, ax,
"1000 Dropout outputs from hand-made NN")
plt.show()
Keras's dropout defenition¶
I will check whether my understanding is correct by creating the same architecture with Keras.
import keras.backend as K
from keras.models import Model
from keras.layers import Input, Dense,Dropout
Nfeat = 1
tinput = Input(shape=(Nfeat,), name="ts_input")
h = Dense(2, activation='relu',name="dense1")(tinput)
hout = Dropout(p_dropout)(h)
out = Dense(1, activation="linear",name="dense2")(hout)
model = Model(inputs=[tinput], outputs=out)
model.summary()
Manually set weight values in the Keras's model¶
for layer in model.layers:
if layer.name == "dense1":
layer.set_weights((w1,b1))
if layer.name == "dense2":
layer.set_weights((w2,b2))
Define a class that do model prediction with dropoff.¶
Keras's prediction function switches off the dropout during prediciton by default. In order to use dropout during prediction, we need to use Keras's backend function. A very clean code is provided as this stack overflow question's answer by Marcin Możejko. I will wrap his code and create a class.
class KerasDropoutPrediction(object):
def __init__(self,model):
self.f = K.function(
[model.layers[0].input,
K.learning_phase()],
[model.layers[-1].output])
def predict(self,x, n_iter=10):
result = []
for _ in range(n_iter):
result.append(self.f([x , 1]))
result = np.array(result).reshape(n_iter,len(x)).T
return result
Predict y with keras's dropout 1000 times¶
kdp = KerasDropoutPrediction(model)
result = kdp.predict(x,Nsim)
ys_keras = result.flatten()
Compare the predicted y from hand-made NN and Keras's NN in terms of the distribution of output y.¶
Both seems to be comparable, indicating that I correctly implemented Keras's dropout function.
fig = plt.figure(figsize=(12,2))
ax = fig.add_subplot(1,2,1)
plot_histogram(ys_handmade, ax,
"1000 Dropout outputs from hand-made NN")
ax = fig.add_subplot(1,2,2)
plot_histogram(ys_keras, ax,
"1000 Dropout outputs from Keras's NN")
plt.show()
Generate synthetic data¶
Now that I understand what actually going on behind Dropout layer of Keras. Let's use it to describe uncertainty of the model following ideas described in Yarin Gal's blog.
I will create a toy 1-d time series for both x and y.
- x : [-2, -1.999, -1.998,...,-1.502,-1.501,-1.500] + [-1.000, -0.999, -0.998,...,0.498,0.499,0.500]
- y : sin(x) - x
Notice that x has a gap between - 1.5 and -1.
import random, math
## Define x
inc = 0.001
x_train =np.concatenate([np.arange(-2,-1.5,inc),np.arange(-1,0.5,inc)])
x_train = x_train.reshape(len(x_train),1)
## Define y
steps_per_cycle = 1
def sinfun(xs,noise=0):
xs = xs.flatten()
def randomNoise(x):
wnoise = random.uniform(-noise, noise)
return(math.sin(x * (2 * math.pi / steps_per_cycle) ) + wnoise)
vec = [randomNoise(x) - x for x in xs]
return(np.array(vec).flatten())
y_train0 = sinfun(x_train)
y_train = y_train0.reshape(len(y_train0),1)
print(" x_train.shape={}".format(x_train.shape))
print(" y_train.shape={}".format(y_train.shape))
Plot the x, y data¶
plt.figure(figsize=(20,3))
plt.scatter(x_train.flatten(),y_train.flatten(),s=0.5)
plt.xlabel("x_train")
plt.ylabel("y_train")
plt.title("The x values of the synthetic data ranges between {:4.3f} and {:4.3f}".format(
np.min(x_train),np.max(x_train)))
plt.show()
Training¶
We consider 4-layer NN. Each hidden layer has relu activation and it is followed by dropout layer.
from keras.models import Model
from keras.layers import Input, Dense,Dropout
from keras import optimizers
def define_model(rate_dropout=0.5,
activation="relu",
dropout_all_hlayers=True):
tinput = Input(shape=(1,), name="ts_input")
Nhlayer = 4
network = tinput
for i in range(Nhlayer):
network = Dense(1024, activation=activation)(network)
if dropout_all_hlayers or i == (Nhlayer - 1):
network = Dropout(rate_dropout)(network)
out = Dense(1, activation="linear")(network)
model = Model(inputs=[tinput], outputs=out)
model.compile(loss="mean_squared_error",
optimizer=optimizers.Adam(lr=0.0001))#0.0005
return(model)
model1 = define_model()
model1.summary()
hist = model1.fit(x_train,
y_train,
batch_size=len(x_train),
verbose=False,
epochs=20000)
Plot the validaiton loss and training loss¶
for key in hist.history.keys():
plt.plot(hist.history[key],label=key)
plt.title("loss={:5.4f}".format(hist.history["loss"][-1]))
plt.legend()
plt.yscale('log')
plt.show()
Create testing data¶
The first half of the testing x contains the x_train, and the second half contains the values outside of the range of x_train
maxx = np.max(x_train)
x_test = np.arange(-2,3 ,inc).reshape(-1,1)
print("x_train -- Min:{:4.3f} Max:{:4.3f}".format(np.min(x_train),maxx))
print("x_test -- Min:{:4.3f} Max:{:4.3f}".format(np.min(x_test),np.max(x_test)))
Prediction with dropout¶
Repeat the prediction with dropout 100 times. As the dropout randomly drop 50% (dropout rate) of the hidden units at every hidden layers, the predicted values vary across the 100 simulations.
kdp = KerasDropoutPrediction(model1)
y_pred_do = kdp.predict(x_test,n_iter=100)
y_pred_do_mean = y_pred_do.mean(axis=1)
Prediction with no dropout¶
y_pred = model1.predict(x_test)
Visualize the descripancies between the prediction without dropout and the average prediction with dropout¶
The two predicted values agree more or less.
plt.figure(figsize=(5,5))
plt.scatter(y_pred_do_mean , y_pred, alpha=0.1)
plt.xlabel("The average of dropout predictions")
plt.ylabel("The prediction without dropout from Keras")
plt.show()
Visualize the prediction with and without dropout on testing data¶
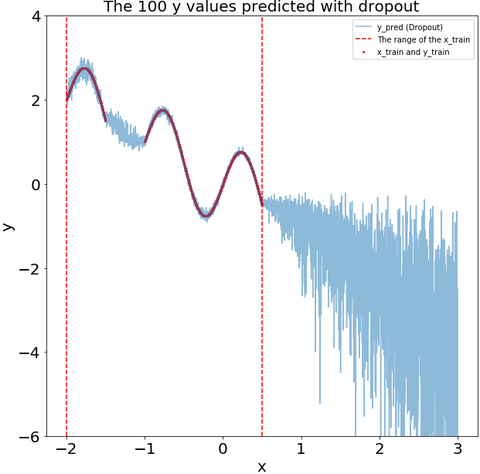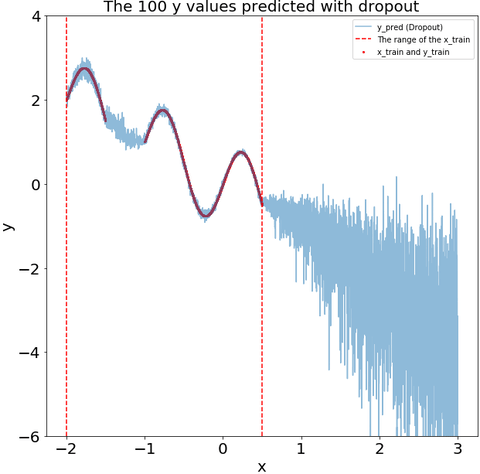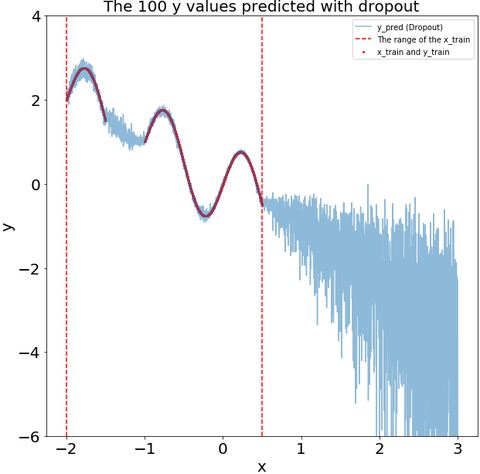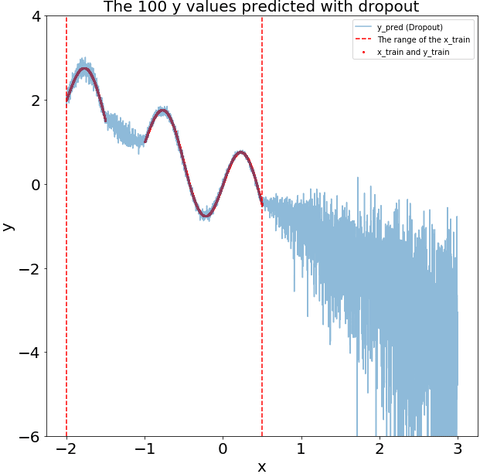
The dropout during the prediction recoginize that some of my test data is far from my training data. i.e., the variance of the dropout prediction increases substantially in the region with no training data.
def vertical_line_trainin_range(ax):
minx, maxx = np.min(x_train), np.max(x_train)
ax.axvline(maxx,c="red",ls="--")
ax.axvline(minx,c="red",ls="--",
label="The range of the x_train")
def plot_y_pred_do(ax,y_pred_do,
fontsize=20,
alpha=0.05,
title="The 100 y values predicted with dropout"):
for iiter in range(y_pred_do.shape[1]):
ax.plot(x_test,y_pred_do[:,iiter],label="y_pred (Dropout)",alpha=alpha)
ax.set_ylim(*ylim)
vertical_line_trainin_range(ax)
ax.set_title(title,fontsize= fontsize)
ylim = (-6,4)
fig = plt.figure(figsize=(18,5))
fig.subplots_adjust( hspace = 0.13 , wspace = 0.05)
ax = fig.add_subplot(1,2,1)
ax.plot(x_test,y_pred,
color="yellow",
label = "y_pred (from Keras)")
ax.scatter(x_test,y_pred_do_mean,
s=50,alpha=0.05,
color="magenta",
label = "y_pred (Dropout average)")
ax.scatter(x_train,y_train,s=2,label = "y_train")
ax.set_ylim(*ylim)
ax.set_xlabel("x")
vertical_line_trainin_range(ax)
ax.legend()
ax = fig.add_subplot(1,2,2)
plot_y_pred_do(ax,y_pred_do)
plt.show()
## location where the png files should be saved
dir_image = "../result/dropout_experiment/"
for icol in range(y_pred_do.shape[1]):
fig = plt.figure(figsize=(10,10))
fig.subplots_adjust(hspace=0,wspace=0)
ax = fig.add_subplot(1,1,1)
plot_y_pred_do(ax,y_pred_do[:,[icol]],
fontsize=20,
alpha=0.5)
ax.scatter(x_train,y_train,s=4,color="red",label="x_train and y_train")
ax.legend()
ax.set_xlabel("x",fontsize=20)
ax.set_ylabel("y",fontsize=20)
ax.tick_params(labelsize=20)
plt.savefig(dir_image + "/fig{:04.0f}.png".format(icol),
bbox_inches='tight',pad_inches=0)
plt.close('all')
Now we are ready to create a gif from the png files¶
def create_gif(gifname,dir_image,duration=1):
import imageio
filenames = np.sort(os.listdir(dir_image))
filenames = [ fnm for fnm in filenames if ".png" in fnm]
with imageio.get_writer(dir_image + '/' + gifname + '.gif',
mode='I',duration=duration) as writer:
for filename in filenames:
image = imageio.imread(dir_image + filename)
writer.append_data(image)
create_gif("dropout_experiment",dir_image,duration=0.1)
How much does the uncertainty change by changing hyper parameters?¶
The hyper parameters to consider are:
- rate_dropout
- activation function for hidden layers
- the location of hidden layers
Some findings:¶
- The variance of the dropout prediction is affected by the hyper parameter values quite a bit for the area with no training data.
- The larger the dropout rate is, the larger the variance of the dropout prediction.
- Nevertheless, all the considered hyper-parameter combination shows that the model is more uncertain in the region with no training data.
- With tanh-activation, the uncertainty seems under estimated in comparisons to the relu-activation. This observation agrees to Yarin Gal's discussion.
rate_dropouts = [0.75, 0.5, 0.1, 0.5, 0.5]
activations = ["relu","relu","relu", "tanh", "relu"]
dropout_all_hlayers = [True, True, True, True, False]
N = len(rate_dropouts)
fig = plt.figure(figsize=(10,N*7))
count = 1
for para in zip(rate_dropouts,activations,dropout_all_hlayers):
model = define_model(*para)
model.fit(x_train,
y_train,
batch_size=len(x_train),
verbose=False,
epochs=20000)
kdp = KerasDropoutPrediction(model)
y_pred_do = kdp.predict(x_test,n_iter=100)
ax = fig.add_subplot(N,1,count)
plot_y_pred_do(ax,y_pred_do,
title="dropout_rate = {}, activation={}, dropout for all layers = {}".format(*para))
count += 1
plt.show()